voriges Kapitel | nächstes Kapitel
Analoge Audioinformationen müssen, um im Computer verarbeitet werden zu können, digitalisiert werden. Eine Digitalisierung ist prinzipbedingt mit Informationsverlusten behaftet, da es sich um eine Diskretisierung eines sonst kontinuierlichen, analogen Signals handelt. Welche Anforderungen an das gewählte Audioformat gestellt werden und welche Einstellungen im Rahmen einer digitalen (verteilten) Audioproduktion einen möglichst geringen Verlust an Informationen bedeutet, wird dieses Kapitel in den einzelnen Unterkapiteln darstellen. (Quelle, sofern nicht anders angegeben: [2]) Darüberhinaus wird betrachtet, welche Speicherplatzanforderungen durch den gewählten Qualitätsmaßstab nötig werden und wie diese Datenmengen vorteilhaft unter den Musikern distribuiert werden können.
3.1 Zeitdiskretisierung
Das analoge, kontinuierliche Audioquellsignal f(t) (siehe Abbildung 8) wird im Analog-Digital Umsetzer der Soundkarte mit einer durch den Anwender festlegbaren Abtastrate (nachfolgend als Samplingrate bezeichnet) abgetastet.
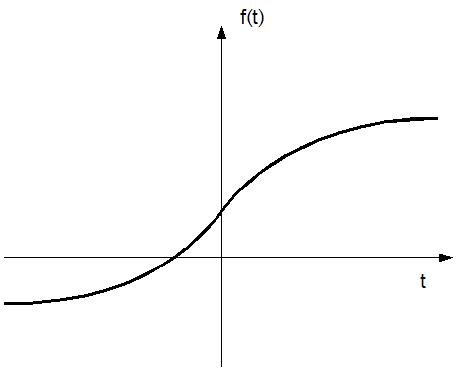
Abbildung 8: Analoges Signal f(t)
Mathematisch betrachtet wird das analoge Signal zu Zeitpunkten auf t mit Dirac Impulsen im Abstand Ta multipliziert. Der Dirac Kamm ist demnach definiert als:
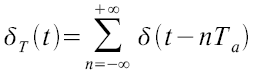
Man spricht auch von einer idealen Abtastfunktion. Abbildung 9 zeigt einen solchen Dirac Kamm (oder auch „Dirac Impulsfolge“).
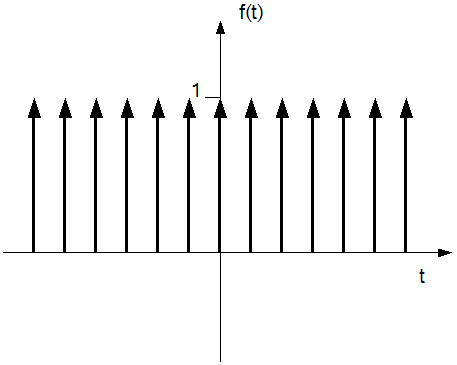
Abbildung 9: Dirac Impulsfolge
Das zeitdiskrete Signal fa(t) ergibt sich demnach als Produkt aus dem analogen Signal f(t) mit der Dirac Impulsreihe δT(t):
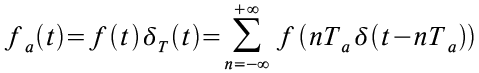
Die resultierende Funktion ist, wie auch der Dirac Kamm selbst, an allen Stellen 0, die nicht diskret sind, also mit einem Dirac Impuls multipliziert wurden. Aus diesem Grunde kann man fa(t) auch als diskrete Folge beschreiben:
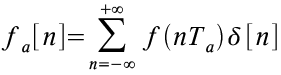
Abbildung 10 zeigt das Ergebnis der Faltung des analogen Signal mit dem Dirac Kamm.
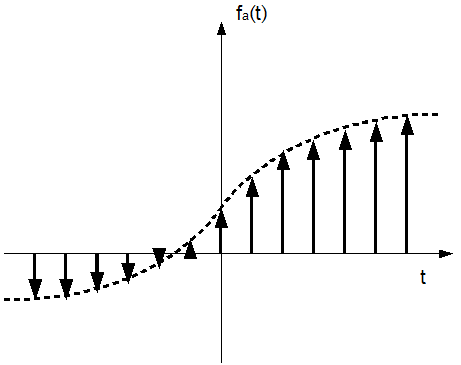
Abbildung 10: Ideale Abtastung durch eine Dirac Impulsfolge
Der Abstand der einzelnen Abtastwerte ist nun entscheidend für die Qualität des digitalisierten Audiosignales und wird in Hertz (Hz) oder Kilohertz (kHz) angegeben. Qualität kann an dieser Stelle verstanden werden als die Ähnlichkeit zwischen dem digitalen Zielsignal und dem analogen Quellsignal im Ohr eines Hörers.
Das sogenannte Nyquist-Shannon-Abtasttheorem (auch Shannonsches Abtasttheorem oder Nyquist Theorem) besagt nun, dass ein kontinuierliches, bandbegrenztes Signal mit einer Minimalfrequenz von 0 Hz und einer Maximalfrequenz von fmax, mit einer Frequenz größer als 2 · fmax abgetastet werden muß, damit man aus dem so erhaltenen zeitdiskreten Signal das Ursprungssignal ohne Informationsverlust exakt rekonstruieren kann (allerdings mit einem unendlich großen Aufwand), bzw. (mit endlichem Aufwand) beliebig genau approximieren kann.
Anders ausgedrückt: wenn ein analoges Signal mit einer Bandbreite von 20 kHz vorliegt (20 Hz bis 20 kHz entspricht dem vom Menschen hörbaren Bereich), dann muß dieses Signal mit mindestens 40 kHz (2 · 20 kHz) abgetastet werden, um sogenannte Alias Effekte zu vermeiden. Andernfalls kann es dazu kommen, dass wichtige, relativ hochfrequente Passagen im analogen Signal zwischen zwei Abtastzeitpunkten des diskreten Signals stattfinden und bei der Rekonstruktion nicht mehr auftauchen, bzw. zu einer Fehlinterpretation führen (dem besagten Alias Effekt). Abbildung 11 zeigt einen Alias Effekt (von [1]):
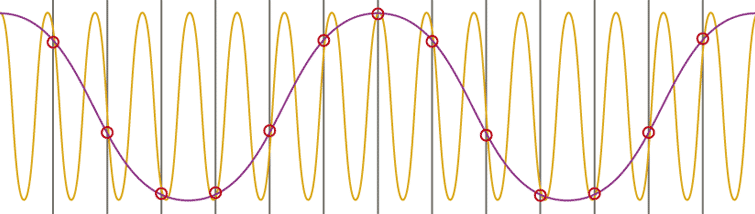
Abbildung 11: Alias Effekt
Die grauen, vertikalen Linien stellen hierbei die diskreten Abtastpunkte dar. Das eigentliche Originalsignal in gelb ist höher frequentiert als die Abtastung. Die Folge ist, dass bei der Rekonstruktion ein Alias Signal (purpur) auftritt, das mit dem Quellsignal wenig Ähnlichkeit hat, aber dieselben Abtastwerte besitzt. Signale einer herkömmlichen Audio CD wurden mit 44,1 kHz gesampelt, entsprechen also dem Anspruch des Nyquist Theorems zu Genüge (44100 Hz > 2 · 20000). Weitere übliche Samplingraten sind beispielsweise 8 kHz, die bei ISDN Telefonie benutzt werden oder 48 kHz, die bei qualitativ höherwertigen Medien (wie zum Beispiel DVD-Audio) zur Anwendung kommen.
Im Audioproduktionsbereich bietet es sich an, während des Produktionsprozesses mit einer möglichst hohe Samplingrate aufzuzeichnen, da jeder vorgenommene Schritt nach der Aufzeichnung die Qualität höchstens erhalten kann. Tatsächlich, so wird das Praxisbeispiel in Kapitel 4 zeigen, kann es darüberhinaus nötig sein, einzelne Passagen dynamisch schneller oder langsamer abspielen zu lassen, um ein musikalisches Tempo einzuhalten, wenn dies dem Quellinstrument (aus verschiedenen Gründen) nicht möglich war. Spätestens in Passagen, die nachträglich langsamer gespielt werden müssen, zahlt sich eine höher gewählte Bitrate aus. Im Rahmen des Beispiels, das in Kapitel 4 behandelt wird, wurde eine Samplingrate von 96 kHz gewählt.
Zur Veranschaulichung zeigt Abbildung 12 einen Zoom auf ein Audiosample in Cubase SX, das zu Anfang (1) in etwa 500 ms lang ist. Die invertierten Bereiche deuten jeweils die Größe des nachfolgenden Zoomfensters an.
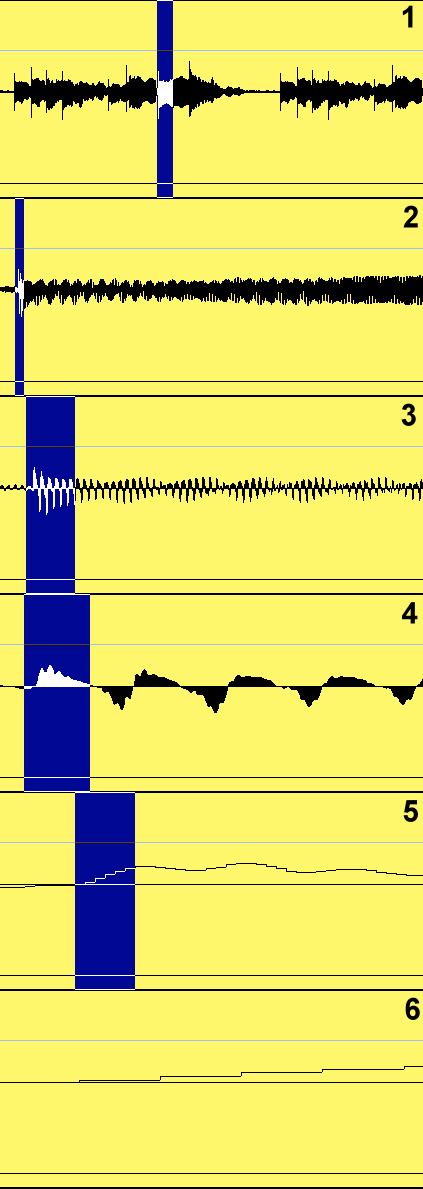
Abbildung 12: Zoom auf ein Audiosample
Zusammenfassend kann man die erforderliche Qualität bei Audioproduktionen auf mindestens 44,1 kHz festlegen, da das fertige Produkt CD Qualität besitzen soll. Deshalb sind für Zuarbeiten anderer Musiker mindestens 44,1 kHz nötig, um nicht unterhalb der bei Audio CDs üblichen Samplingrate zu kommen. Trotzdem gilt: je höher die Samplingrate in der Produktion ist, desto besser. Allerdings bedeutet die doppelte Samplerate auch die doppelte Datenmenge und stellt so gewisse Anforderungen an Festplatten- und Computergeschwindigkeit. Die Datenmenge errechnet sich nun aus dem Produkt aus Samplerate und Bitrate.
3.2 Amplitudenquantisierung
Zusätzlich zur Samplerate, die bislang das analoge Audiosignal lediglich in eine bestimmte Anzahl gleichgroßer Abschnitte unterteilt hat, müssen natürlich auch die entsprechenden Werte der Amplitude digital gespeichert werden. Das bedeutet, dass auch hier diskretisiert werden muß. Da die Amplitude (also die Stärke des Ausschlags der Schwingung) innerhalb des Computers ebenfalls nur durch eine endliche Anzahl von Digitalwerten ausgedrückt werden kann, entstehen Rundungsfehler, die unter Umständen bei einer Wiedergabe des Signals als sogenanntes Quantisierungsrauschen hörbar werden. Wie hoch die endliche Anzahl von Digitalwerten ist, ermittelt sich über die Bitrate, die jedem Sample eine bestimmte Anzahl Bits zugesteht.
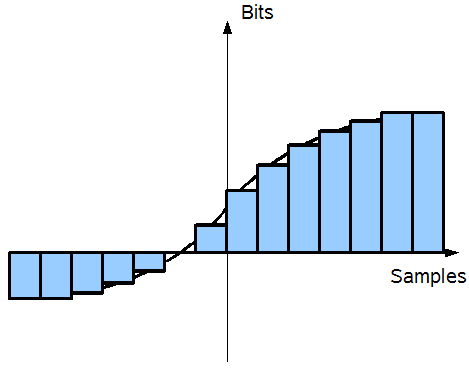
Abbildung 13: Quantisierungsrauschen
Abbildung 13 veranschaulicht die Problematik: für jedes Sample mit einer festen Breite (je breiter, desto kleiner die Samplerate und umgekehrt) muß ein digitaler Wert gefunden werden (hier in der Höhe der Samples dargestellt), der dem Originalsignal (als Linie dargestellt) am nächsten kommt. Die maximale Anzahl verschiedener Digitalwerte ermittelt sich über die Anzahl Bits, die jedem Samples zur Verfügung stehen. 8 Bit bedeutet beispielsweise, dass es pro Sample maximal 256 (= 28 = 8 Bit) verschiedene Zustände geben kann. Je nach Analogsignal kann es sein, dass diese Granularität nicht ausreicht, um das Signal auf der digitalen Basis zufriedenstellend zu reproduzieren. Entsprechend besser wären 16 Bit, denn dies würde eine 256 mal so feine Auflösung bedeuten. Die qualitätsmindernden Unterschiede zwischen Analog- und Digitalsignal nennt man Quantisierungsrauschen und diese kann qualitativ durch die Signal-to-Noise Ratio angegeben werden.
Die Signal-to-Noise Ratio (SNR), zu deutsch etwa das Signal-Rausch Verhältnis, ist definiert als das Verhältnis der vorhandenen mittleren Signalleistung σX zur vorhandenen mittleren Rauschleistung σE. Als Verhältnis von Größen gleicher Maßeinheit ist das Signal-Rausch Verhältnis dimensionslos.
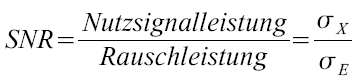
Da die Signalleistung aber gewöhnlicherweise weitaus größer ist, als die Rauschleistung, wird die SNR oft im logarithmischen Maßstab dargstellt, mit der Einheit Bel, bzw. Dezibel.

Um nun errechnen zu können, wie groß das Rauschen (in dB) ist, das durch eine Quantisierung mit N Bit entsteht, muß man zunächst den Quantisierungsschritt q des A/D Wandlers bestimmen. Die Vollaussteuerung entspricht der doppelten Amplitude A. Ein Umsetzer mit N Bit hat somit einen Quantisierungsschritt von
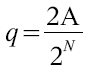
Der Quantisierungsfehler pro Schritt wird angenommen als gleichmäßig verteilt über das Intervall -q/2 bis +q/2. Damit ist die Leistungsdichte zufolge der Quantisierung gegeben als:
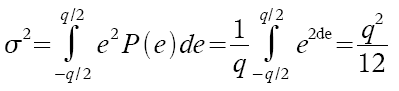
Sigma drückt das Störsignal der Quantisierung aus, welches das Rauschen verursacht. Das Eingangssignal mit Vollpegel hat eine mittlere Leistung von:
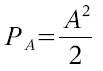
Diese Werte kann man nun in die SNR Gleichung einsetzen:
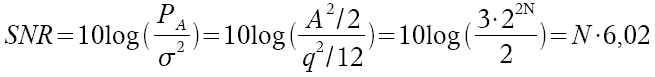
Verkürzt ausgedrückt: um den Rauschabstand in einem Signal mit N Bit zu berechnen, benötigt man folgende Gleichung:
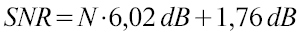
Der Signal-Rausch Abstand bei 8 Bit beträgt also 8 · 6,02 + 1,76 = 49,92 dB. Bei 16 Bit sind es entsprechend 98,08 dB und bei 24 Bit 146,24 dB. (Pro Bit also in etwa 6 dB.)
Da der Mensch bei etwa 120 bis 140 dB seine Schmerzschwelle in Bezug auf Lautstärke hat, kann man annehmen, dass bei einem mit 24 Bit gesampelten Signal in keinem Fall ein Rauschen erkennbar sein wird.
3.3 Resultierende Speicheranforderungen
Wie in den letzten beiden Kapitel gezeigt wurde, lässt sich die Qualität eines digitalisierten Audiosignales anhand der beiden Größen Sampling- und Bitrate beschreiben. Dabei gilt, dass höhere Werte grundsätzlich und prinzipbedingt eine höhere Qualität bedeuten (wobei Qualität in diesem Falle die Ähnlichkeit zwischen dem analogen Quellsignal und dem digitalen Zielsignal im Ohr des Hörers beschreibt). Wie aber ebenfalls gezeigt wurde, machen gewisse Raten ab bestimmten Punkten keinen Sinn mehr, wenn man unterstellt, dass das Audiosignal für menschliche Ohren digitalisiert wurde, die ihrerseits gewissen Beschränkungen unterliegen. Diese sind nach [3] die maximal noch schmerzfrei zu ertragenden Lautstärke, die mit etwa 130 dB angegeben wird und die für den Menschen hörbare Bandbreite von etwa 20 Hz bis 20 kHz.
Höhere Bitraten als 24 Bit sind also unnötig, da der Abstand zwischen Nutzsignal und Quantisierungsrauschen größer als die akustische Schmerzschwelle des Menschen ist (man muß bedenken, dass 10 dB mehr aufgrund des logarithmischen Maßstabes im subjektiven menschlichen Hörempfinden einer Verdopplung der Lautstärke entspricht). In einem mit 24 Bit aufgezeichneten Audiosignal kann der Mensch demnach kein kodierungsbedingtes Rauschen mehr hören. Voraussetzung ist natürlich, dass das Audiosignal an seiner lautesten Stelle mit genau 0 dB (Vollaussteuerung) aufgezeichnet wurde. In der Praxis lässt man gewöhnlicherweise das lauteste Signal bei etwa -5 dB ausgesteuert (der sogenannte Headroom oder zu deutsch auch Übersteuerungsreserve). Aber auch 141 dB sind noch weit über der Schmerzschwelle anzusiedeln. Wenn nun allerdings mehrere Spuren gleichzeitig (schwach) rauschen, kann das zusammengemischte Endprodukt durchaus ein wahrnehmbares Rauschen produzieren. Entsprechend bieten sich die 24 Bit bei der Aufnahme an, um diese Rauschsummation so gering wie möglich zu halten. Wenn es nur darum geht, eine einzelne Audiospur wiederzugeben, reichen 16 Bit (98,08 dB) vollkommen aus, denn selbst die beste analoge Endstufe kann wohl kaum mehr als 100 dB Rauschabstand wiedergeben.
Ebenso ist eine Samplingrate im fertigen Endprodukt, die mehr als doppelt so groß ist, wie der vom Menschen insgesamt hörbare Bereich, aufgrund des Nyquist Theorems nicht sinnvoll. Während des Produktionsprozesses jedoch kann es sehr wohl Sinn machen, die Samplingrate höher zu wählen, um zum Beispiel unter Umständen die Möglichkeit zu besitzen, Signale langsamer abspielen zu lassen, ohne dass darunter die Qualität deutlich hörbar leidet.
Der einzige Punkt, der gegen hohe Bit- oder Samplingraten spricht, ist der Speicherplatzbedarf und die gegebenenfalls nicht ausreichende Geschwindigkeit des Studiocomputers, der in vielen Fällen eine Vielzahl von voneinander unabhängigen Audiosignalen in Echtzeit abspielen können muß.
Eine Minute eines mit 44,1 kHz und 16 Bit kodierten Audiosignals summiert sich auf 42336000 Bit Speicherbedarf. Das sind 5292000 Byte oder 5,04 Megabyte. Eine 8 Bit Kodierung würde entsprechend genau die Hälfte, nämlich 2,52 Megabyte beanspruchen. Eine Minute 96 kHz, 24 Bit benötigen schon 16,48 Megabyte.
Ein dreiminütiger Durchschnittssong in der Produktion benötigt also bei 7 verschiedenen Instrumenten (siehe Abbildung 3 auf Seite 11) 346,07 Megabyte (7 · 3 · 16,48 MB) Speicherkapazität. Zusätzlich bedeutet dies, dass die Festplatte, auf der die Daten gespeichert sind, mindestens 1,9 Megabyte pro Sekunde (15,38 Mbit/sec) lesen können muß, um alle Spuren in Echtzeit wiederzugeben. Bei entsprechender Fragmentierung der Festplatte müssen ebenso die Zugriffszeiten entsprechend hoch sein. In der Praxis sind die Anforderungen an den Rechner meist noch höher, da es mehrere Takes zu verschiedenen Instrumenten gibt und besonders Echtzeiteffekte und VST-Instrumente (dazu später mehr) die Kapazitäten der CPU und der Festplatte beanspruchen.
Für moderne Rechner stellen diese Werte keine nennenswerte Hindernisse dar, jedoch sehr wohl für die Distribution der Zwischenprodukte zwischen beteiligten Musikern und dem Produzenten, wie in einem Szenario von Abbildung 5 angedeutet. Während es zwar sinnvoll und auch empfehlenswert ist, die Audiodaten, die bereits im Studio hochwertig vorliegen, mit einem verlustbehafteten Format (zum Beispiel MP3 oder Ogg Vorbis) zu kodieren und zu verschicken, damit beteiligte Musiker dazu ihren Teil aufnehmen können, darf der umgekehrte Weg der Aufnahme vom Musiker zum Studio nicht verlustbehaftet sein.
Verlustbehaftete Audioformate sind qualitativ gut genug, um einem Musiker die nötige Begleitung für seine Arbeit zu liefern und ebenso das Tempo präzise vorzugeben, allerdings wäre es wohl kaum wünschenswert, eine MP3 Datei in eine Spur eines Audioprojekt zu importieren, da stets das qualitativ schlechteste Audiosample die höchstmögliche Qualität des Endproduktes determiniert. (Eine Kette ist so stark wie ihr schwächstes Glied!)
Aus diesem Grunde sollte die Zuarbeit der Musiker im WAV-, im AIFF- (beide jeweils mit unkomprimierten PCM-Rohdaten) oder im FLAC-Format (komprimiert aber nicht verlustbehaftet) ans Studio zurückgeschickt werden. Welchen verlustfreien Audiocodec man dafür verwendet, ist letztlich eine Geschmacksfrage, allerdings sollten sowohl Bitrate als auch Samplingrate dem restlichen Projekt aus oben angeführten Gründen entsprechen.
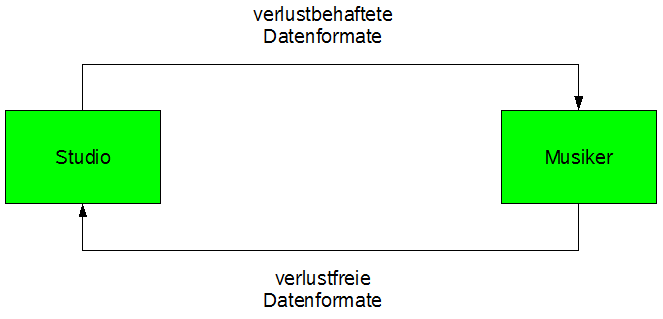
Abbildung 14: Effizienter Datenaustausch
Abbildung 14 stellt den optimalen Datenaustausch zwischen Studio und Musiker dar: während das Studio die Sounddateien, die zur Arbeit des Musikers nötig sind, im ressourcenschonenden, aber verlustbehafteten Format verschickt, versendet der Musiker seiner fertige Arbeit, die ins Endprodukt einfließen soll, in jedem Fall verlustfrei.
3.4 Sinnvolle Distributionswege und -arten für digitales Audiomaterial
Im Idealfalle benutzt ein Musiker, der seinen Teil zum Audioprojekt hinzufügen muß, dieselbe Software, dasselbe Betriebssystem und arbeitet mit demselben Audioprojekt, das dem letzten Stand aus dem bearbeitenden Studio entspricht. Dies ist in der Praxis jedoch erstens höchst selten der Fall und zweitens erscheint es auch sehr aufwendig, das gesamte Projekt zu verschicken. Jedem beteiligten Musiker eine eigene gebrannte CD zukommen zu lassen (oder je nach Projektgröße sogar eine DVD) und diese in regelmäßigen Abständen durch neue Versionen zu aktualisieren, verschwendet nicht nur Ressourcen, sondern ist auch höchst arbeitsaufwendig. Auch wiederbeschreibbare Wechselmedien wie USB-Sticks oder Speicherkarten besitzen den Nachteil, dass sie immernoch physikalisch ausgetauscht werden müssen, d.h. entweder von Angesicht zu Angesicht überreicht oder von der gelben Post nach einigen Tagen zugestellt werden.
Von daher bietet sich das Internet als geeignet erscheinender Kanal für die Verteilung von Arbeitsversionen in besonders hohem Maße an: die Zustellung geschieht weltweit sofort und gegebenenfalls für eine kaum beschränkte Anzahl von beteiligten Musikern. Der Nachteil der Speicherplatzanforderungen, der im letzten Kapitel angedeutet wurde, besteht aber nach wie vor, wodurch Verteilungen im Anhang von E-Mails in der Regel nur bei einzelnen MP3 Dateien mit wenig Megabyte sinnvoll erscheinen. Größere Datenmengen, wie insbesondere Audiodateien, die in das Projekt einfliessen sollen und von daher verlustfrei sein müssen, können nur in wenigen Fällen per E-Mail verschickt werden, da die meisten Mailprovider Beschränkungen der Anhangsgröße technisch vorgeben und darüberhinaus das SMTP (Simple Mail Transfer Protocol) aufgrund seiner Kodierung von 7-bit ASCII [4] wenig geeignet für ressourcenschonende Datendistribution ist.
Eine Alternative stellt ausreichender Webspace (sofern vorhanden) dar, der allerdings vor unbefugten Zugriffen geschützt sein sollte. Die Daten können dann per FTP auf einen Server hochgeladen und zeitversetzt vom Musiker, bzw. dem Studio heruntergeladen werden.
Wenn man bereit ist, seine Daten einem anderen Unternehmen anzuvertrauen, bieten sich die zahlreichen Sharehoster (auch bekannt als One-Click Hoster oder Filehoster) an, bei denen man gewisse Datenmengen ohne vorherige Anmeldung hochladen und diese danach über einen (prinzipiell geheimen) URL wieder beziehen kann. Diese müßte dann lediglich mit den Musikern oder dem Studio kommuniziert werden.
Der im Jahre 2007 gestartete Dienst Dropbox bietet seinen Nutzern kostenlos 2 Gigabyte Speicherplatz. Die hochgeladenen Daten können entweder für Freunde oder für alle freigegeben werden. Aufgrund der Speicherkapazität und dem Schutz der Daten auf Benutzernamenbasis erscheint dieser Dienst derzeit als besonders geeignet für asynchronen Austausch großer Datenmengen (2 GB entsprechen immerhin mehr als 2 Stunden unkomprimiertem Audiomaterial, das mit 96 kHz und 24 Bit gesampelt ist).
Als synchrone Variante wäre an dieser Stelle noch die üblicherweise in fast allen Clients enthaltene Dateitransfermöglichkeit der Instant Messenger zu nennen. Hier werden die Daten direkt zwischen zwei Parteien ausgetauscht, ohne sie auf einem Server zwischenzulagern. Der Nachteil besteht hauptsächlich in der Funktionalität, die oft durch Firewall- oder Routereinstellungen beeinflußt wird und in der Notwendigkeit, den Start des Transfers mit dem Empfänger abzusprechen.
Es ist zu erwarten, dass in Zukunft (und mit steigender Bandbreite für Internetanschlüsse) noch weitere komfortable Möglichkeiten zum direkten Datenaustausch geschaffen werden. Für die im Rahmen der Audioproduktion nötigen Schritte sind heutige Techniken aber schon mehr als geeignet, wie auch das folgende Kapitel zeigen wird.
voriges Kapitel | nächstes Kapitel



