Hörbare Signale haben eine bestimmte Frequenz. Der Kammerton A, der gewöhnlicherweise auch das Freizeichen in deutschen Telefonen gibt, hat 440 Hz und wird zum Stimmen von Instrumenten genutzt.
Die Frequenz des nächsten Tones auf der chromatischen Tonleiter berechnet sich als
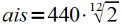. Damit hat also der Ton A#1 eine rein rechnerische Frequenz von präzise 466,16376151808991640720312977628 Hz. Das H muß entsprechend mit etwa 493 Hz erklingen, das C mit ungefähr 523 Hz, usf. (Allerdings werden Instrumente aufgrund der entstehenden Obertöne leicht abweichend gestimmt, zum Beispiel das wohltemperierte Klavier.)Bestimmte klassische Instrumente haben natürlich auch eigene Wirkungsbereiche für ihre charakteristischen Frequenzen. Folgende wunderbare Abbildung verdeutlicht das.
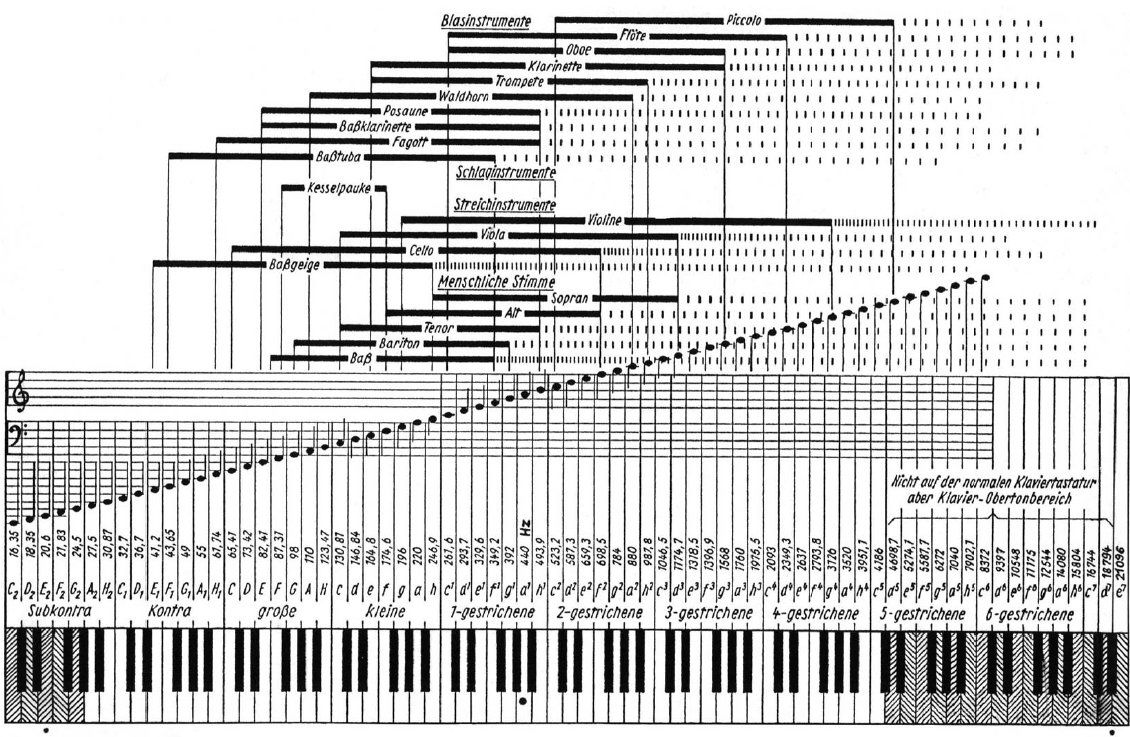
Frequenzbereiche klassischer Instrumente (aus 8)
Dem menschlichen Gehör ist eine Reichweite von etwa 20 kHz (also 0 - 20000 Hz) gegeben.
Wer nicht mehr weiß, wie man die x-te Wurzel berechnet oder den entsprechenden Knopf in seinem Taschenrechner nicht findet, der benutzt lieber diese Formel: 
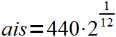
Mit derselben Formel lassen sich übrigens auch die Abstände der Bünde der Gitarre berechnen, nur sollte man natürlich statt den Hertz die Länge des vorhergehenden Bundes einsetzen und da die Bünde nach oben hin kleiner werden, muß man dividieren und nicht multiplizieren. Beispiel: der Abstand zwischen Bund 0 und Bund 1 der Gitarre beträgt 3,6 cm, also ist der Abstand zwischen Bund 1 und Bund 2 3,39 cm lang.
